Epidemiology is not only about tracking diseases, it is about understanding patterns and relationships between causes and outcomes. Every news report about public health, whether it covers air pollution, vaccine guidelines, or disease monitoring, often relies on the work of epidemiologists. Their role combines observation, analysis, and statistical reasoning to make sense of health data.
From air quality–related asthma in children to evaluating the effectiveness of medical treatments, each case requires systematic investigation. This investigation begins with careful measurement and interpretation of data, which is where biostatistics plays a central role.
Real World Contexts Where Epidemiology Applies
Let us consider a few examples that reflect the wide scope of epidemiologic work:
- Environmental health: Increased smog levels in an inner city are linked to more asthma attacks among children and older adults.
- Chronic disease management: A young person with type I diabetes achieves better blood sugar control after a course of traditional Chinese medicine.
- Preventive health: Federal recommendations for flu vaccination change to include more groups.
- Disaster response: A city hit by a hurricane strengthens its disease surveillance systems.
- Occupational and chemical exposure: A scientific study reports that certain chemicals may increase cancer risk.
In each example, epidemiologists collect and analyze data to estimate the level of risk, compare outcomes, and decide whether observed differences are likely due to chance or reflect real effects.
Types of Epidemiologic Measurements
Epidemiologic investigations often begin with two main types of statistical measurements.
- One sample measurements
These focus on how often a condition or event occurs in a group. Examples include the rate of asthma in a neighborhood or the prevalence of diabetes in a community. - Two sample measurements
These compare two groups to see if there is a relationship between exposure and outcome. Examples include comparing the risk of cancer among workers exposed to a chemical versus those who were not exposed.
Measures of occurrence are typically one sample measures, while measures of association, such as the risk ratio (RR) or the odds ratio (OR), are two sample measures.
Point Estimates. The Starting Place
A point estimate is a single value that represents your best guess of the true measure in a population based on your sample data.
For example, if you find that 15 out of 100 children in your study have asthma, your point estimate for prevalence is 15 percent.
- One sample measures include rates, risks, and prevalence.
- Two sample measures include risk ratios and odds ratios.
Point estimates are the basis for epidemiologic inferences. They tell you what you observed, but not how precise that observation is.
Confidence Intervals. Measuring Precision
A confidence interval (CI) gives a range of values within which the true population value is likely to fall.
Precision depends on three key factors:
- Natural variability of the measure. For instance, height varies less than weight across a population, so height estimates tend to be more precise.
- Random measurement error such as variation between instruments or between technicians taking the measurements.
- Sample size where larger samples produce narrower, more precise confidence intervals.
For example, if your point estimate for asthma prevalence is 15 percent with a 95 percent CI of 12 percent to 18 percent, you can be reasonably confident that the true value lies within that range.
Comparing to a Reference Value
Often, biostatistics is used to check whether a point estimate is consistent with a known or expected reference value. This is where hypothesis testing comes in.
You begin with a null hypothesis that assumes no difference or no effect. You then calculate a p value, which is the probability of observing your data, or something more extreme, if the null hypothesis were true.
If the p value is smaller than your chosen significance level, often written as ![]() , you reject the null hypothesis.
, you reject the null hypothesis.
Type I and Type II Errors
Statistical testing can lead to two types of errors:
- Type I error: Rejecting a true null hypothesis. This means you conclude there is a difference when there is none. If
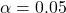 , there is a 5 percent chance of making this error.
, there is a 5 percent chance of making this error. - Type II error: Failing to reject a false null hypothesis. This happens when there is a real difference but your test fails to detect it. The probability of this error is
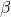 .
.
The power of a study is ![]() , which is the probability of detecting a meaningful difference when it truly exists.
, which is the probability of detecting a meaningful difference when it truly exists.
The Role of Effect Size
Before starting a study, you should define what constitutes a meaningful difference. This is the effect size you want to detect.
For example, if a new asthma intervention would be considered successful only if it reduces attacks by at least 20 percent, then 20 percent is your minimum effect size of interest. Power calculations use this value to determine how many participants you need.
Determining Sample Size
Sample size decisions depend on the type of measure and the study purpose.
For one sample measures:
- Descriptive studies: Choose a sample size that gives the desired CI width.
- Hypothesis testing: Calculate the sample size needed to detect a meaningful difference from a reference value while controlling Type I and Type II errors.
For two sample measures:
- Decide the smallest difference in rates or risks between groups that would be considered meaningful.
- Use statistical formulas that incorporate
 ,
, 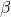 , expected variability, and the effect size.
, expected variability, and the effect size.
For example, to detect a difference in disease prevalence between two communities, you would need more participants if the expected difference is small, and fewer if the difference is large.
Bringing It All Together
In practice, epidemiologists use these principles every day:
- Measuring asthma prevalence after a smog event is a one sample measure.
- Comparing cancer rates between exposed and unexposed groups is a two sample measure.
- Calculating confidence intervals shows how precise the estimates are.
- p values help decide whether observed differences are likely due to chance.
- Sample size and power calculations ensure the study can detect meaningful effects.
The combination of these steps allows for evidence based decisions in public health, from policy changes to targeted interventions.
