Quantiles are values that split a dataset into equal parts. They are useful when you want to understand how data is spread out. Quartiles divide data into four equal sections, tertiles into three, quintiles into five, deciles into ten, and percentiles into one hundred equal sections.
For example, if you have cholesterol readings from 100 people, the 50th percentile is the point where half the people have lower cholesterol and half have higher cholesterol. This single number can give you a quick sense of the middle of your data.
Common Types of Quantiles
While quantiles all follow the same principle, some are used more often in health and statistical studies.
- Quartiles: Divide the data into four equal parts
- Tertiles: Divide the data into three equal parts
- Deciles: Divide the data into ten equal parts
- Percentiles: Divide the data into one hundred equal parts
For example, in infant growth charts, you may see curves for the 5th, 50th, and 95th percentiles of weight. These are calculated from large datasets and help show where an individual child’s growth stands compared with a reference population.
How to Calculate a Quantile
Let us say you want to find the ![]()
![]() -tile, where
-tile, where ![]() . Suppose your dataset has
. Suppose your dataset has ![]() values, sorted from smallest to largest.
values, sorted from smallest to largest.
The steps are:
- Compute the position using:
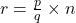
- If
 is not an integer, round it up to the next highest integer
is not an integer, round it up to the next highest integer  and take the value
and take the value 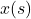 .
. - If
 is an integer, take the average of
is an integer, take the average of 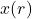 and
and 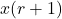 .
.
Here ![]() means the
means the ![]() smallest value in your dataset.
smallest value in your dataset.
Finding the Median
The median is the second quartile, so ![]() and
and ![]() .
.
Suppose ![]() cholesterol readings. Then:
cholesterol readings. Then:
![]()
Since 25 is an integer, the median is:
![]()
This means you take the 25th and 26th values in the ordered list and find their average.
First Quartile
Using the same ![]() , for the first quartile
, for the first quartile ![]() ,
, ![]() :
:
![]()
Since this is not an integer, round up to 13. The first quartile is ![]() , the 13th value in the ordered list.
, the 13th value in the ordered list.
Tertiles in a Small Dataset
Let us take a small dataset:
3, 3, 7, 8, 9, 11, 14, 15, 20
Here ![]() .
.
- First tertile position:

Since 3 is an integer,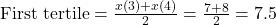
- Second tertile position:

Since 6 is an integer,
These tertiles split the data into three equal parts: 3 values below the first tertile, 3 between the two tertiles, and 3 above the second tertile.
Practical Uses of Quantiles
Quantiles are not just about describing data.
1. Identifying Risk Groups
In public health, percentiles can help define high-risk populations. For example, if the 90th percentile of cholesterol is 240 mg/dL, you know the top 10 percent of the population has cholesterol above this level. This helps target prevention programs.
2. Comparing Distributions
When you have data from two sources, you can compare them using a quantile–quantile (Q-Q) plot. This involves plotting the same quantiles from one dataset against the other.
If the points fall on a straight line, the two distributions are similar. If they curve away from the line, their shapes differ. This gives a quick visual check, similar to comparing two boxplots but often with more detail.
3. Growth and Clinical Reference Charts
In pediatrics, growth charts mark weight-for-age or height-for-age percentiles. A child at the 50th percentile is average for their age. A child at the 5th percentile is smaller than 95 percent of their peers.
Comparing with Boxplots
A boxplot is another way to show quartiles visually. It displays the median, the first and third quartiles, and the spread of the data.
However, quantiles go further. They allow you to look beyond quartiles into finer divisions, such as deciles or percentiles. This can be useful in detailed clinical studies where small differences matter.
Quantile Types and Examples
| Quantile Type | Division | Example in Health Data |
|---|---|---|
| Quartiles | 4 parts | Median cholesterol or 25th, 50th, 75th percentiles |
| Tertiles | 3 parts | Splitting BMI data into low, medium, high |
| Deciles | 10 parts | Grouping patient risk scores into ten equal sections |
| Percentiles | 100 parts |