HEOR Analytics • Updated On August 26, 2025

Standardization – Direct and Indirect Methods with Examples

Death and disease rates rise with age, and they often differ between women and men. If two communities have different mixes of age and sex, their overall rates cannot be compared at face value. A community with more older adults will show a higher crude mortality rate even if each age group has the same risk as the other community. You need a method that removes these structural differences so that the comparison is fair.

What standardization does

Standardization gives you adjusted measures that neutralize major confounders, most often age and sex. The idea is simple, you combine age specific rates with a reference population so that both groups are evaluated on the same footing. You can do this in two ways, called direct and indirect standardization. Both use a standard population, but they swap what gets applied to what.

Direct standardization: apply the study group age specific rates to the standard population to get an adjusted rate.
Indirect standardization: apply the standard age specific rates to the study population to get expected counts and an SMR, also called a standardized mortality or morbidity ratio.

Notation and key formulas

Use a single scaling constant for rates such as K equals one hundred thousand for easy reading. Let the age group index be j. Let r_j^study be the study group age specific rate, N_j^std be the standard population count in age group j, and R_j^std be the standard age specific rate. Let n_j^study be the study group population count in age group j, O be the observed number of events, and E be the expected number of events.

Direct standardized rate $\displaystyle \text{DSR}=\frac{\sum_{j} r_{j}^{\text{study}}\times N_{j}^{\text{std}}}{\sum_{j} N_{j}^{\text{std}}}\times K$
Expected events for indirect method $\displaystyle E=\sum_{j}\left(\frac{R_{j}^{\text{std}}}{K}\times n_{j}^{\text{study}}\right)$
Standardized mortality or morbidity ratio $\displaystyle \text{SMR}=\frac{O}{E}\times 100$
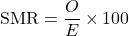
Indirect standardized rate using the crude rate of the standard population $\displaystyle \text{ISR}=\left(\frac{\text{SMR}}{100}\right)\times R^{\text{std}}_{\text{crude}}$

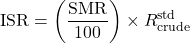
Direct standardization

When to prefer direct standardization

Choose direct standardization when you have reliable age specific rates for each study group. It works very well when the counts are not tiny in any age band, since the rates then have acceptable precision. It is the best choice when you want a single adjusted rate per group for easy side by side comparison. You can also extend it to adjust for other factors, for example ethnic group.

Worked example for direct standardization

Assume a standard population of one hundred thousand people with three age bands. Ages zero to thirty nine, fifty thousand people. Ages forty to sixty four, thirty thousand people. Ages sixty five and above, twenty thousand people.

Study group A age specific rates per one hundred thousand
- Ages zero to thirty nine, eighty
- Ages forty to sixty four, three hundred
- Ages sixty five and above, one thousand two hundred
Study group B age specific rates per one hundred thousand
- Ages zero to thirty nine, one hundred
- Ages forty to sixty four, two hundred eighty
- Ages sixty five and above, one thousand

Compute expected events in the standard population if each group had its rates. For group A the counts are forty, ninety, and two hundred forty, which sum to three hundred seventy. Divide by one hundred thousand, then multiply by one hundred thousand, and you get a direct standardized rate of three hundred seventy per one hundred thousand. For group B the counts are fifty, eighty four, and two hundred, which sum to three hundred thirty four, so the adjusted rate is three hundred thirty four per one hundred thousand.

On these adjusted rates group B looks better, even though the crude rates might have shown the opposite if group A had more young people. Direct standardization made the footing equal by using the same age structure for both groups. That is the entire goal. You matched on the distribution that drives the risk.

Indirect standardization

When to prefer indirect standardization

Use indirect standardization when study group age specific rates are unstable or unavailable, for example when you have small numbers or short follow up. It is also helpful when you can easily get trustworthy standard rates from a national registry. The primary product is the SMR, which says how the observed events compare to what would be expected if the study group had the same age specific rates as the standard. You can also convert the SMR to an adjusted rate for communication.

Set up the example

Keep the three age bands. Now define two study populations with different age structures. Group A has sixty thousand people in ages zero to thirty nine, twenty five thousand in ages forty to sixty four, and fifteen thousand in ages sixty five and above. Group B has forty thousand, thirty five thousand, and twenty five thousand in those same bands.

Suppose standard age specific rates per one hundred thousand are ninety, two hundred ninety, and one thousand one hundred for the three age bands. Suppose the observed age specific rates for group A are eighty, three hundred, and one thousand two hundred, the same as the earlier direct example. Suppose the observed age specific rates for group B are one hundred, two hundred eighty, and one thousand. We can compute observed events and expected events.

Observed events for group A
- Ages zero to thirty nine, forty eight
- Ages forty to sixty four, seventy five
- Ages sixty five and above, one hundred eighty
- Total observed O equals three hundred three
Expected events for group A using standard rates
- Ages zero to thirty nine, fifty four
- Ages forty to sixty four, seventy two point five
- Ages sixty five and above, one hundred sixty five
- Total expected E equals two hundred ninety one point five

Now compute the SMR for group A. $\displaystyle \text{SMR}_{A}=\frac{303}{291.5}\times 100\approx 104$ Group A has about four percent more events than expected under the standard. You can turn this into an adjusted rate if you know the crude rate of the standard population.

Compute the crude rate of the standard population using its own age mix of fifty thousand, thirty thousand, and twenty thousand. Expected events are forty five, eighty seven, and two hundred twenty, which sum to three hundred fifty two. So the crude standard rate is three hundred fifty two per one hundred thousand. The indirect standardized rate for group A is then $\displaystyle \text{ISR}_{A}=\left(\frac{104}{100}\right)\times 352 \approx 366$

Observed events for group B
- Ages zero to thirty nine, forty
- Ages forty to sixty four, ninety eight
- Ages sixty five and above, two hundred fifty
- Total observed O equals three hundred eighty eight
Expected events for group B using standard rates
- Ages zero to thirty nine, thirty six
- Ages forty to sixty four, one hundred one point five
- Ages sixty five and above, two hundred seventy five
- Total expected E equals four hundred twelve point five

The SMR for group B is $\displaystyle \text{SMR}_{B}=\frac{388}{412.5}\times 100\approx 94$ So group B has fewer events than expected. Its indirect standardized rate is $\displaystyle \text{ISR}_{B}=\left(\frac{94}{100}\right)\times 352 \approx 331$ These values line up with the direct results in direction and size, which adds confidence.

Uncertainty for the SMR

A quick approximate interval for the SMR uses the log scale. The standard error is $\displaystyle \text{SE}\big(\ln(\text{SMR})\big)=\frac{1}{\sqrt{O}}$ A ninety five percent interval is $\displaystyle \exp\left(\ln(\text{SMR})\pm 1.96\times \text{SE}\right)$ For group A with O equals three hundred three, the interval is roughly ninety three to one hundred sixteen percent.

Choosing the standard population

Pick a population that is relevant to your question and large enough to be stable. You can use a national census, a regional registry, or the combined study populations if that makes scientific sense. The choice affects the numeric value of the adjusted rate, but it does not usually change the direction of the comparison. Always report what you used so that others can reproduce your numbers.

Direct versus indirect, how to decide

Use direct standardization when you have reliable age specific rates in each study group and you want a single adjusted rate for each group.
Use indirect standardization when age specific counts are sparse, when some rates are unstable, or when you need a summary relative measure such as the SMR.
Both methods can be extended to adjust for sex, ethnicity, calendar period, or other structural variables by expanding the set of strata.
For formal testing across multiple groups, consider Mantel and Haenszel methods or a Poisson regression that includes age and sex terms.

Common pitfalls and how to avoid them

Mixing denominators

Keep the scaling constant K consistent across all calculations. If your rates are per one hundred thousand, do not switch to per one thousand in the middle of a computation. Convert everything to the same base first. You will avoid silent errors that are hard to spot later.

Too many narrow strata with tiny counts

Standardization can become unstable when you slice the data into very fine age bands with very small numbers. Combine adjacent bands to keep expected and observed counts reasonable. Your adjusted results will be smoother and more trustworthy. You will also avoid zero cells that cause division issues.

Using crude rates after adjustment

Do not compare a crude rate from one group to a standardized rate from another group. Once you adjust, you should compare adjusted to adjusted or SMR to SMR. Otherwise you bring back the confounding that standardization was meant to remove. Be deliberate and consistent.

Forgetting to document the standard

Always name the standard population and the year. Report the age bands and any other stratification used. If you present SMRs, state the expected counts so others can evaluate the stability. Clear documentation makes your work repeatable.

Short workflow you can follow

Define the purpose of comparison and the key confounders such as age and sex.
Choose the standard population, list the age bands, and fix the value of K.
Compute age specific rates for each study group if possible. If not possible, collect good quality standard rates.
Run direct standardization if rates are reliable. Otherwise compute expected counts and SMRs with the indirect method.
Optionally convert SMRs to adjusted rates by multiplying by the crude rate of the standard population.
Report adjusted values, confidence intervals when needed, and the full specification of the standard.

How this relates to regression and stratified methods

Standardization gives you clean descriptive measures that are easy to communicate. When you need to test for differences or adjust for many variables at once, you can move to stratified estimators such as Mantel and Haenszel, or use Poisson regression with age and sex terms. These approaches model the rates and give standard errors and P values in a single framework. They complement, rather than replace, standardized summaries.

Extra example, adjusting a mean with the direct method

Standardization is not only for rates. You can compute a standardized mean, for example an age adjusted mean blood pressure for several occupational groups. Replace the age specific rate r_j^study with the age specific mean m_j^study. Use the same direct formula to combine the means with the standard population weights.

Direct standardized mean $\displaystyle \text{DSM}=\frac{\sum_{j} m_{j}^{\text{study}}\times N_{j}^{\text{std}}}{\sum_{j} N_{j}^{\text{std}}}$

Here is the checklist

Name of the standard population and year.
Age bands and any other strata such as sex or ethnicity.
Scaling constant K and unit, for example per one hundred thousand.
Adjusted rates for each group if you used the direct method.
Observed counts, expected counts, and SMRs if you used the indirect method.
Confidence intervals for SMRs or for adjusted rates when available.