Likelihood is a concept in statistics that measures how well a specific value of a parameter explains the observed data. In epidemiology and clinical research, you often want to estimate a probability or risk—for example, the risk of disease transmission or the effectiveness of a treatment.
The likelihood of a particular value of that risk tells you how “compatible” that value is with the data you observed. The higher the likelihood, the more the data support that value.
Think of likelihood as a way of asking: “If the true risk was X, how likely am I to see the results I got in my study?” By comparing likelihoods for different values of X, you can find which value makes the observed results most probable. This approach forms the basis of maximum likelihood estimation (MLE), a widely used method to estimate unknown parameters in medicine and public health.
Maximum Likelihood Estimate (MLE) Explained
The maximum likelihood estimate (MLE) is the value of the parameter that gives the highest likelihood for the observed data. In other words, it is the value that makes your data most “expected” or most likely.
Statisticians choose the parameter value that maximizes the likelihood function (a function that calculates the probability of the data for each parameter value).
The MLE is essentially the peak of the likelihood function.
It is the parameter value for which your data have the greatest probability of occurring.
In many simple cases, the MLE coincides with familiar statistics like the sample mean or sample proportion. This is not a coincidence—these sample statistics are often the values that maximize the likelihood in basic scenarios.
Once you have the MLE, you treat it as your best estimate of the true underlying parameter (like a true risk or true probability) given the data.
It’s important to note that while the MLE is the most likely value, there is still uncertainty; other values might also be reasonably likely, which we will explore through confidence intervals and likelihood ratios in later sections.
Example Scenario: TB Transmission in Households
Let’s illustrate likelihood with a practical example. Suppose a study is investigating household transmission of tuberculosis (TB). You have an index TB patient and 12 of their close household contacts who all get tested for TB infection. Out of these 12 contacts, 3 test positive for TB infection (perhaps via a tuberculin skin test or IGRA), and the other 9 test negative.
We want to estimate the risk of TB transmission within the household, which we’ll call p (the probability that a given household contact becomes infected).
So in our sample:
- n = 12 household contacts tested.
- d = 3 contacts tested positive (assumed infected due to household exposure).
- h = 9 contacts tested negative (not infected).
The sample proportion of positives is
Intuitively, it makes sense that our best estimate of the true household transmission risk p would be 25% based on this sample. The concept of likelihood will confirm this intuition by showing that p = 0.25 is indeed the value most supported by the data.
Calculating the Likelihood
To formally find the MLE, we consider the likelihood function for our data. Since each contact either became infected or not, this is a scenario we can model with a binomial probability distribution. The likelihood of observing exactly 3 positives out of 12 (with 9 negatives) for a given transmission probability p is:
where 
is the combinatorial term (the number of ways to choose which 3 out of 12 are positive). This formula comes from the binomial distribution. It essentially says: the probability of any specific arrangement of 3 positives and 9 negatives is 
, and there are such arrangements. So 
gives the probability of getting exactly 3 positives and 9 negatives as a function of the unknown true probability 
.
We treat this probability as a function of —that is our likelihood function.
Now, to find the maximum likelihood estimate, we need to see which value of maximizes . We could plug in different values of between 0 and 1 and see what is:
- If
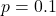(10%), 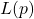will be relatively low because it would be unlikely to see as many as 3 positives out of 12. - If
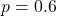(60%), 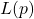will also be low because we would expect more than 3 positives out of 12. - If
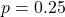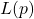, is higher. In fact, it is maximized at 0.25.
Mathematically, one can take the derivative of or its log-likelihood and set it to zero to solve for the maximizing .
But without calculus, we can reason: the likelihood peaks at
In general, for binomial data, the MLE for the probability of success is the sample proportion.
If you were to plot against from 0 to 1, you would see a curve that rises, reaches a maximum at 0.25, and then falls off. This shows that 25% is the value of the household transmission risk that makes the observed outcome most likely.
Interpreting the MLE in Context
By finding the MLE, we conclude that the most likely true risk of TB infection for a household contact in this scenario is 25%. In practical terms, if similar conditions hold, we would estimate that about one in four close contacts of a contagious TB case will be infected through household exposure. This estimate is based on the observed data and is the one that best aligns with our results.
However, this does not mean the true risk is exactly 25%—it could be a bit lower or higher. The MLE is our single best estimate, but we also need to consider uncertainty around this estimate. In epidemiology, we often provide a confidence interval to show a range of plausible values for the true risk. We might also assess how strongly the data support values near 25% versus values quite different from 25%. These ideas can be approached using likelihood ratios and confidence intervals, which we will explore in another article.