You often compare two groups by looking at the difference between two proportions. This quantity is called the risk difference when the outcome is a risk, yet the same methods apply to any proportion. With a two by two table you can estimate the difference, build a confidence interval, and test whether the population difference is zero. The influenza vaccine example below shows every step in a simple and reproducible way.
Set up the two by two table the right way
Previously we saw the two by two table advantage. Place the exposure in rows and the outcome in columns, then fill the four cells with counts. Keep notation tidy so you can move from counts to proportions without confusion. Use d for the number with the event, use h for the number without the event, and use n for totals. Add subscripts one for exposed and zero for unexposed to keep groups distinct.
Notation and basic proportions
- Group totals are n1 and n0, overall total is n.
- Events are d1 and d0, non events are h1 and h0.
- Proportions are
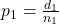 ,
,  , overall proportion is
, overall proportion is  .
.
Sampling distribution for the difference between two proportions
The sample difference ![]() estimates the population difference, and it varies from sample to sample. When sample sizes are large enough, the normal model is a good approximation for this difference. A practical rule is that
estimates the population difference, and it varies from sample to sample. When sample sizes are large enough, the normal model is a good approximation for this difference. A practical rule is that ![]() ,
, ![]() ,
, ![]() , and
, and ![]() should each be at least ten. This becomes more accurate as these counts grow.
should each be at least ten. This becomes more accurate as these counts grow.
Mean and standard error of the difference
The sampling mean equals the population difference, so it centers on the true value. The standard error combines uncertainty from both groups. Use the following formula to compute it from the two sample proportions and sizes.
![]()
Confidence interval for the difference between two proportions
A confidence interval gives a range of plausible population differences. With the normal model you take the estimate and add and subtract a z multiple of the standard error. For a ninety five percent interval you use z equal to one point nine six.
![]()
Influenza vaccine example, confidence interval
Suppose two hundred forty people received vaccine and two hundred twenty people received placebo. Twenty people in the vaccine group developed influenza and eighty people in the placebo group developed influenza. Proportions are ![]() and
and ![]() , the observed difference equals
, the observed difference equals ![]() .
.
The standard error is ![]() The ninety five percent interval is
The ninety five percent interval is ![]() This equals
This equals ![]() You can say the vaccine reduces absolute risk by about twenty one percent to thirty five percent in this study population.
You can say the vaccine reduces absolute risk by about twenty one percent to thirty five percent in this study population.
Hypothesis test for a zero difference between two proportions
You may want to test whether the population difference equals zero. The z statistic divides the observed difference by a pooled standard error that assumes equal population proportions. The pooled estimate uses the total number of events over the total number of participants.
![]()
![]()
Influenza vaccine example, z test and P value
The overall proportion is ![]() The pooled standard error is
The pooled standard error is ![]() The test statistic is
The test statistic is ![]()
The two sided P value is less than 0.0001, which is far below common decision thresholds. You would conclude that the risk in the vaccine group is lower than the risk in the placebo group. Report both the P value and the confidence interval, since together they convey strength and size of effect.
Conditions for using the normal approximation
The normal method is accurate when counts in each outcome cell are not too small. A simple rule is that ![]() ,
, ![]() ,
, ![]() , and
, and ![]() are at least ten when you use the pooled test. If these are smaller, consider a continuity corrected approach or an exact test based on the hypergeometric model. For very small samples the exact method is safer.
are at least ten when you use the pooled test. If these are smaller, consider a continuity corrected approach or an exact test based on the hypergeometric model. For very small samples the exact method is safer.
Presenting results with clarity and context
Always present the difference between two proportions as both an absolute change and a relative change when possible. Readers need the absolute number to understand practical impact, while the relative number shows strength of association. State the table totals, the counts, and the proportions, then add the interval and the test result.
Tips that improve interpretation
- Show the two by two table so your audience can see the raw information.
- Report
 ,
, 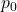 , and
, and 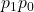 with sensible rounding, three decimals are often enough.
with sensible rounding, three decimals are often enough. - Include the z statistic, the P value, and the ninety five percent confidence interval.
