Confidence Intervals for ICER, INB, and ACER

Research updated on July 29, 2025
Cite: Biopharma Foundry. (2026, Month Day). Article title in italics. Article link
Author: Santhosh Ramaraj

When healthcare decision-makers evaluate new treatments, the key question is not just about clinical outcomes but also whether the treatment offers value for money. Cost-effectiveness analysis (CEA) provides this insight. Among its most commonly used tools are the Incremental Cost-Effectiveness Ratio (ICER), Incremental Net Benefit (INB), and Average Cost-Effectiveness Ratio (ACER).

The ICER measures the additional cost required to gain one unit of effectiveness, such as one Quality-Adjusted Life Year (QALY), when moving from one treatment to another. The INB translates this tradeoff into a monetary metric, factoring in how much a payer is willing to pay for a unit of health gain. The ACER shows the average cost per unit of effectiveness within a single treatment group.

However, point estimates of ICER or INB alone do not tell the full story. They can be misleading if there is high variability in cost or effectiveness data. Confidence intervals are needed to assess uncertainty and to guide decisions. For example, two cancer drugs may have similar mean costs and QALYs, but one may be far more uncertain due to skewed cost distributions. Previously we saw the definitions. In this guide, we explore how to calculate confidence intervals for ICER, INB, and ACER, with step-by-step explanations.

Basic Definitions

Suppose we are comparing two treatments, Treatment 1 and Treatment 2. Let:

$C_j$ = Cost for patients in group j (j = 1, 2),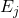
$E_j$ = Effectiveness measure (e.g., QALYs) for group j (j = 1, 2).

The population mean cost and effectiveness are:

$\mu_{C_j} = E[C_j], \quad \mu_{E_j} = E[E_j]$

ICER

The Incremental Cost-Effectiveness Ratio is defined as:

$ICER = \frac{\mu_{C_1} - \mu_{C_2}}{\mu_{E_1} - \mu_{E_2}}$

This tells us the additional cost per unit of health gain when switching from treatment 2 to treatment 1.

INB(λ)

To avoid the drawbacks of ratios like ICER (especially when the denominator is close to zero), analysts often use the Incremental Net Benefit (INB). INB requires a willingness-to-pay threshold (λ), which reflects how much a decision-maker is willing to pay per unit of effectiveness:

$INB(\lambda) = \lambda (\mu_{E_1} - \mu_{E_2}) - (\mu_{C_1} - \mu_{C_2})$

A positive $INB(\lambda)$ means treatment 1 is cost-effective compared to treatment 2 at the chosen threshold.

ACER and ΔACER

The Average Cost-Effectiveness Ratio (ACER) is calculated for a single treatment:

$ACER = \frac{\mu_C}{\mu_E}$

For comparing two treatments, we use the incremental ACER (ΔACER):

$\Delta ACER = \frac{\mu_{C_1}}{\mu_{E_1}} - \frac{\mu_{C_2}}{\mu_{E_2}}$

The Need for Confidence Intervals

While computing the above point estimates is easy, it is critical to measure their uncertainty. For instance, if the ICER is $20,000 per QALY, but the confidence interval ranges from -$5,000 to $70,000, the interpretation changes drastically.

In practice, cost and effectiveness data come from randomized controlled trials (RCTs) or real-world studies. These data are subject to variability due to patient differences, sampling errors, and other confounders. Therefore, constructing confidence intervals around ICER, INB, and ACER allows executives and payers to make more robust and defensible decisions.

Common Approaches for Confidence Intervals

There are several methods used in the literature to derive confidence intervals:

Fieller’s theorem
Taylor series expansion (Delta method)
Bootstrap methods (parametric and nonparametric)
Bayesian methods
Generalized pivotal quantities

Each method has trade-offs. Below, we discuss them in detail.

Fieller’s Theorem

Fieller’s theorem is a classical approach for confidence intervals of ratios like ICER. It assumes that the differences in costs and effects are normally distributed. The main advantage of Fieller’s method is that it accounts for the ratio structure directly.

However, Fieller’s theorem can produce infinite or undefined intervals when the denominator (difference in effectiveness) is very close to zero. For example, if two treatments have almost identical effectiveness but very different costs, the ICER becomes unstable.

Example:
Suppose the mean cost difference is $\bar{C}_1 - \bar{C}_2 = 1000$ and the mean effectiveness difference is $\bar{E}_1 - \bar{E}_2 = 0.05$ QALYs. Then:

$ICER = \frac{1000}{0.05} = 20,000 , \text{USD per QALY}$

Fieller’s theorem would use the variance and covariance of these means to construct a confidence interval.

Taylor Series Expansion (Delta Method)

The delta method linearizes complex functions (like ratios) using a Taylor series expansion. If $\hat{\theta}$ is an estimator and $g(\hat{\theta})$ is a function of that estimator, then:

$Var[g(\hat{\theta})] \approx (g'(\hat{\theta}))^2 Var(\hat{\theta})$

For ICER, the delta method approximates the variance of $\frac{\mu_C}{\mu_E}$ by considering first-order derivatives of the cost and effect means. It is computationally simpler but less accurate if the denominator is small or data is skewed.

Bootstrap Methods

The bootstrap is widely used in health economics because it does not require strict distributional assumptions. It works by resampling the original dataset (with replacement) many times (e.g., 1,000 or 10,000 iterations) and recalculating ICER or INB for each resample. The resulting empirical distribution is then used to construct confidence intervals.

Step-by-Step Bootstrap Example:

Take the migraine dataset with costs and QALYs for two treatments.
Resample 1,000 times, each time calculating ICER.
Sort the 1,000 ICER estimates and take the 2.5th and 97.5th percentiles for a 95% CI.

This approach is intuitive and works well even when costs are skewed or sample sizes are moderate.

Bayesian Approaches

Bayesian methods incorporate prior knowledge about costs and effects into the analysis. Instead of a single point estimate, Bayesian analysis produces a posterior distribution for ICER or INB. Confidence intervals (called credible intervals in this framework) are then derived from this posterior distribution.

For example, if historical data suggests that the average cost difference is around $1,000 with some uncertainty, this prior information can be combined with trial data to produce more realistic estimates.

When Data Are Lognormal

Cost data are often lognormal because medical costs tend to have long right tails. In such cases, a log-transformation is applied. Assume that $\ln C_j$ is normally distributed with mean $\mu_{lC_j}$ and variance $\Sigma_{11_j}$ . The mean cost is then:

$\mu_{C_j} = \exp \left( \mu_{lC_j} + \frac{1}{2} \Sigma_{11_j} \right)$

The ICER can be expressed as:

$ICER = \frac{ \exp \left( \mu_{lC_1} + \frac{1}{2} \Sigma_{11_1} \right) - \exp \left( \mu_{lC_2} + \frac{1}{2} \Sigma_{11_2} \right) }{ \mu_{E_1} - \mu_{E_2} }$

Example: Migraine Drug Comparison

Consider two migraine treatments:

Treatment A: Mean cost = $4,000, mean effectiveness = 2.5 QALYs.
Treatment B: Mean cost = $3,000, mean effectiveness = 2.0 QALYs.

The ICER is:

$ICER = \frac{4000 - 3000}{2.5 - 2.0} = \frac{1000}{0.5} = 2000 , \text{USD per QALY}$

Suppose the willingness-to-pay threshold is $\lambda = 50,000$ . Then:

$INB(50000) = 50,000 \times (2.5 - 2.0) - (4000 - 3000) = 25,000 - 1,000 = 24,000$

A positive INB means Treatment A is cost-effective compared to Treatment B.

Advanced Concepts: CEAC and CEAF

The Cost-Effectiveness Acceptability Curve (CEAC) plots the probability that a treatment is cost-effective against different values of $\lambda$ . The Cost-Effectiveness Acceptability Frontier (CEAF) shows which treatment is most likely to be optimal at each willingness-to-pay threshold.

For example, using bootstrap results, we can calculate $P[\hat{INB}(\lambda) > 0]$ for various $\lambda$ and plot it to form a CEAC. A CEAC that rises above 0.8 at a threshold of $50,000 per QALY means there is an 80% chance the treatment is cost-effective.

Practical Tips

Use multiple methods: Check results with both bootstrap and delta methods.
Visualize uncertainty: Plot CEACs and scatter plots of cost vs. effectiveness differences.
Interpret ICER carefully: Pay attention when the denominator (effectiveness difference) is small.
Work with INB: INB is easier to interpret and compare across λ values.
Run sensitivity analyses: Explore how results change with different assumptions.

Relevant Reads