Direct and Indirect Age Adjustment in Death Rates

Research updated on August 8, 2025
Cite: Biopharma Foundry. (2026, Month Day). Article title in italics. Article link
Author: Santhosh Ramaraj

When you compare death rates between different geographic areas, the age makeup of each population can distort the results. For instance, imagine comparing two towns. One has a younger population, the other has many older residents. Even if the disease risk is the same for each age group, the town with more older people will naturally show a higher overall death rate.

If you ignore this and just compare crude rates, you might wrongly assume that the older town is less healthy. Age adjustment removes this bias. It allows you to compare rates on an equal footing, as if both populations had the same age distribution.

There are two main ways to adjust for age: direct standardization and indirect standardization. Each has its own uses, advantages, and limitations.

Direct Age Adjustment. The Basics

In direct age adjustment, you take the age specific death rates from your study population and apply them to a standard population’s age distribution.

Think of it this way, instead of comparing the actual age structure of your area, you ask: What would the death rate be if this area had the same age distribution as the standard population?

This produces what is called the Directly Age Adjusted Death Rate (DAADR).

The formula is:

$\text{DAADR} = \sum W_{si} \times \frac{D_i}{P_i} = \sum W_{si} \times R_i$

$W_{si}$ = weight for age group i in the standard population (proportion of standard population in that group)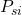
$P_{si}$ = population in age group i in the standard population
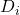$D_i$ = number of deaths in age group i in the study population
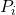$P_i$ = population in age group i in the study population
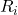$R_i$ = age specific rate for group i in the study population

Example

Suppose the standard population has 20 percent in age group 0 to 44, 30 percent in age group 45 to 64, and 50 percent in age group 65 and above.
You calculate the age specific death rate for each group in your study population.
Multiply each death rate by the corresponding standard population weight.
Add them up to get your directly age adjusted death rate.

Calculating Variance and Standard Error for DAADR

Since the number of deaths in each age group follows a Poisson distribution, we can calculate the variance for each age specific death rate:

$\text{var}(R_i) = \frac{R_i^2}{D_i}$

The variance for the DAADR is:

$\text{var(DAADR)} = \sum W_{si}^2 \times \frac{R_i^2}{D_i}$

The standard error is:

$SE(\text{DAADR}) = \sqrt{\text{var(DAADR)}}$

This standard error is important when constructing confidence intervals. Many statistical software packages can calculate these automatically using gamma distribution factors.

When to Use Direct Age Adjustment

You have enough events in each age group
Population sizes are large enough to give stable age specific rates
You want to compare multiple areas to each other on an equal basis

However, when event counts are very small in some groups, indirect adjustment is often more reliable.

Indirect Age Adjustment. A Practical Alternative

If your study population is small, you might have very few cases in some age groups, sometimes only one or two. This can make age specific rates unstable and misleading.

As a general rule, if your study population has fewer than about 20 to 25 total events, indirect standardization is preferred.

How Indirect Adjustment Works

Instead of applying your own age specific rates to the standard population, you apply the standard population’s age specific rates to your study population’s age distribution.

This gives the expected number of deaths in your population if it experienced the same rates as the standard population. You then compare the actual number of deaths to this expected number using the Standardized Mortality Ratio (SMR):

$\text{SMR} = \frac{D}{e} = \frac{\text{Observed deaths}}{\text{Expected deaths}}$

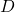$D$ = observed number of deaths in the small area
$e$ = expected number of deaths = 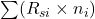$\sum (R_{si} \times n_i)$
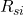$R_{si}$ = age specific death rate for group i in the standard population
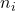$n_i$ = population count in group i in the study population

The indirectly standardized rate is:

$\text{ISR} = \text{SMR} \times R_s$

Where $R_s$ is the crude death rate in the standard population.

Example of Indirect Adjustment

Standard population death rate for age 65+ is 40 per 1,000, and for age under 65 is 5 per 1,000.
Your small area has 500 people over 65 and 1,000 under 65.
Expected deaths = (40 × 500 / 1,000) + (5 × 1,000 / 1,000) = 20 + 5 = 25.
If your area actually had 30 deaths, SMR = 30 / 25 = 1.2.
If the crude death rate in the standard population is 8 per 1,000, ISR = 1.2 × 8 = 9.6 per 1,000.

Calculating Confidence Intervals for Indirect Rates

When the Number of Events is 20 or More

$\text{CI}_{\text{ISR}} = \pm 1.96 \times \sqrt{\frac{\text{SMR}}{e}} \times R_s \times K$

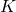$K$ is the constant used to express the rate (e.g., 100,000 for rates per 100,000 population)

When the Number of Events is Fewer than 20

Use Poisson table limits for observed deaths:

Lower limit:

$\text{LL}_{\text{ISR}} = \frac{\text{Poisson lower limit for D}}{e} \times R_s \times K$

Upper limit:

$\text{UL}_{\text{ISR}} = \frac{\text{Poisson upper limit for D}}{e} \times R_s \times K$

Key Differences Between Direct and Indirect Adjustment

Direct Method – Compares multiple areas with each other, requires stable age specific rates, needs sufficient events in each group
Indirect Method – Compares only to the standard population rate, works well when events are small, uses standard population age specific rates

Choosing the Right Method

If your dataset is large and event counts are sufficient in each age category, direct age adjustment is the best option for fair comparisons across regions.

If you are working with small populations or rare events, indirect adjustment provides more stable results. You can still explain results in simple terms by interpreting the SMR. For example, an SMR of 1.2 means the observed deaths are 20 percent higher than expected if the population had the same age specific rates as the standard.

Relevant Reads