When studying disease patterns, it is important to distinguish between the rate and the risk. A rate relates the number of new events to the total time that people were observed. Risk, also called cumulative incidence, relates the number of new events to the number of people who were at risk at the start of the observation period.
The longer you follow people, the higher the risk will appear, because more events have time to occur. Risk therefore has an implicit time element, while the rate makes the time element explicit. Understanding the difference is essential when you compare populations with different follow up lengths.
How Disease Accumulates Over Time
Imagine two populations that are completely free of a particular disease at the start. Both groups are followed for five years. In one group, the disease rate is high at 0.3 per person per year. In the other group, the rate is much lower at 0.03 per person per year.
If surveillance is complete, meaning no one migrates and no one is lost to follow up, the two populations will show very different patterns of disease accumulation. The high rate leads to a rapid decline in the disease free population, while the low rate results in a gradual decline.
Exponential Decline with High Rates
When the incidence rate is high, the proportion of disease free individuals decreases quickly. The process works in a way that is similar to compound interest in finance. At each moment, the disease rate operates on the remaining disease free individuals. Since that number is shrinking, the count of new cases per unit of time becomes smaller and smaller.
This explains why the cumulative incidence does not rise in a straight line but instead slows its growth as time passes. The relationship is captured mathematically by an exponential function.
Mathematical Representation
- Proportion still disease free at time t:
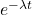
- Risk of disease up to time t:
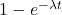
- Average time until disease occurs:
Linear Appearance with Low Rates
When the incidence rate is low, the disease free population declines slowly. Over short periods, the exponential curve looks almost like a straight line. This makes the accumulation of risk appear nearly constant.
In such cases, the risk of disease up to time t is well approximated by multiplying the rate by time. This simplification is often used in practice when dealing with rare conditions.
Approximation for Small Rates
When 
is very small:
This means the rate is roughly equal to the value of risk divided by time.
Practical Example with Numbers
Let us calculate the risk for two different rates.
- For a rate of 0.3 per person per year, the risk after one year is
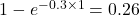. After two years, the risk is 0.45. After five years, the risk rises to 0.78. - For a rate of 0.03 per person per year, the risk after one year is only 0.03. After two years it is 0.06, and after five years it is 0.14.
This shows that a high rate leads to rapid accumulation early on, while a low rate results in a steady, nearly linear increase.
Interpreting the Relationship Between Rate and Risk
It is important to note that the risk is always less than the rate multiplied by time. This is because the number of people at risk is shrinking over time. For example, with a rate of 0.3 per year, the risk after one year is 0.26 instead of 0.3. After two years, it is 0.45 instead of 0.6. After five years, it is 0.78 instead of 1.5.
The difference between the actual risk and the simple rate times time is more noticeable at higher rates. At lower rates, the two values are very close.
The Formal Definition of a Rate
The concept of a rate can be defined more precisely. If you take the risk of disease over a very short time period and divide it by the length of that period, the value approaches the rate. This happens because in a tiny interval, the number of people at risk has not had time to decrease much.
Mathematically:
Numerical Illustration
Consider again a rate of 0.3 per person per year. If you look over a five year interval, the average risk per year is only 0.155, well below the true rate. Over one year, the risk per year rises to 0.259, closer but still less than 0.3.
As the time interval gets shorter, the risk divided by time approaches 0.3. At one month, the value is 0.296. At one week, it is 0.299. At one day, it is 0.2999. At one hour or one minute, the number is effectively identical to the rate of 0.3.
Table Example with Rate of 0.3 per Person per Year
| Interval Length | t (in years) | Risk =  |
Risk / t |
|---|---|---|---|
| 5 years | 5 | 0.7769 | 0.1554 |
| 1 year | 1 | 0.2592 | 0.2592 |
| 1 month (30 days) | 0.08219 | 0.02436 | 0.2963 |
| 1 week | 0.01918 | 0.005737 | 0.2992 |
| 1 day | 0.002740 | 0.0008216 | 0.2999 |
| 1 hour | 0.0001142 | 0.00003420 | 0.3000 |
| 1 minute | 0.000001900 | 0.0000005710 | 0.3000 |
Applications in Biostatistics
These concepts have many practical applications in biostatistics. For example:
- In cancer epidemiology, high rates of relapse make exponential decline highly relevant when estimating survival curves.
- In infectious disease modeling, low rates of infection allow for linear approximations when forecasting incidence over short periods.
- In clinical trials, accurate understanding of rate versus risk prevents overestimation of treatment effects when follow up times differ.
By carefully distinguishing between rate and risk, and by applying exponential or linear approximations as appropriate, you can interpret your study results with much greater accuracy.