Epidemiology / HEOR Analytics / Observational Data Analytics

Likelihood-Based Hypothesis Testing

We often form a null hypothesis (e.g., “no difference between groups” or “no association between risk factor and outcome”) and then test if the data provide evidence against it. Traditionally, we compute a test statistic and a p-value. If the p-value is below a chosen threshold (like 0.05), we say the result is statistically significant, meaning the data are unlikely under the null hypothesis and thus we have evidence to reject the null.

Likelihood methods provide elegant ways to conduct these tests. There are three main approaches derived from the likelihood framework:

  • Likelihood Ratio Test (LRT)
  • Wald Test
  • Score Test

All three tests will, in large samples, often agree closely. But there are situations where they differ, and it’s useful to know the distinctions. Let’s break them down using the example from Article 4 (the respiratory infection rate ratio) for illustration, where our null hypothesis might be that the rate ratio \theta = 1 (no difference between housing conditions).

Likelihood Ratio Test (LRT)

The likelihood ratio test compares the maximum likelihood under the null hypothesis to the maximum likelihood under the alternative hypothesis. The test statistic is:

\text{LRT statistic} = -2 \ln\Big(\frac{\text{Likelihood at null}}{\text{Likelihood at MLE}}\Big) = -2[\ln L(\text{null}) - \ln L(\text{MLE})]

This statistic, when the sample size is large, follows a \chi^2 (chi-square) distribution with degrees of freedom equal to the number of parameters being tested (for a single parameter like a rate ratio, df = 1). The intuition: if the null hypothesis is true, forcing that parameter to the null value should not drastically decrease the likelihood. If the data strongly contradict the null, the maximum likelihood under the alternative will be much bigger than under the null, making the LRT statistic large.

For the rate ratio example:

  • Under the null (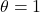\theta = 1), the best 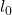l_0 is the combined rate: (33+24)/(355+518).
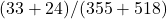  • Under the alternative, we already found the MLE: \theta=2.01, l_0 = 24/518.

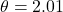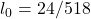From article, the log-likelihood values were approximately:

  • L_{\text{null}} \approx -42.2211
  • L_{\text{MLE}} \approx -38.7956

The log-likelihood ratio is L_{\text{null}} - L_{\text{MLE}} \approx -3.4255. Multiplying by -2: \text{LRT} = 6.851.

This corresponds to a p-value around 0.009. This low p-value indicates strong evidence against the null (i.e., the rate ratio is not 1; housing does affect infection rates).

The LRT is very robust. A big advantage is invariance: testing \theta=1 or \log(\theta)=0 gives the same result.

Wald Test

The Wald test uses the MLE and its standard error. If \hat{\theta} is the MLE and SE(\hat{\theta}) is its standard error, then to test H_0: \theta = \theta_0:

Z = \frac{\hat{\theta} - \theta_0}{SE(\hat{\theta})}

Often we use the log scale. In our example, \hat{u} = \ln(2.01) = 0.698 with SE(\hat{u}) = 0.268. The Wald statistic is:

Z = 0.698/0.268 = 2.60

This corresponds to a two-tailed p-value near 0.0094. Squaring Z gives Z^2 = 6.76, close to the LRT value (6.85).

The Wald test essentially asks: is the estimate far enough from the null in terms of SEs? It works well in large samples, especially on the log scale for ratios. But it can be less reliable if the parameter is near a boundary, the sample is small, or if done on the raw scale instead of log.

Score Test

The score test (Lagrange Multiplier test) looks at the slope of the log-likelihood at the null. If the slope is large, the null is unlikely. If the slope is near zero, the null may be plausible.

The score statistic can be written as:

\text{Score test statistic} = \frac{U^2}{V}

where U is the score (first derivative of log-likelihood at the null) and V is the information (second derivative at the null). This follows a \chi^2 distribution with df = 1.

In practice, common chi-square tests and Mantel-Haenszel tests can be interpreted as score tests. In our example, the score test around \theta=1 would yield a chi-square near 6.8, with a similar p-value to the LRT and Wald.

When to Use Which?

  • Likelihood Ratio Test: Preferred for multiple parameters or model comparisons. Invariant to scaling, reliable with adequate sample size.
  • Wald Test: Convenient for individual parameters in fitted models. Every regression output usually includes Wald tests. May misbehave near boundaries or in small samples.
  • Score Test: Useful when evaluating at the null without fitting the full model. Handy in model building or when MLEs are hard to compute.

In large samples, all three tend to agree. Big discrepancies suggest assumptions may not hold, and exact or resampling methods may be better.

Example: Does Treatment Improve Survival?

Imagine a clinical trial comparing drug vs placebo on 1-year survival. Null hypothesis: equal survival rates.

  • LRT: Compares likelihood under equal vs different survival rates.
  • Wald: Uses the survival difference or odds ratio estimate divided by its SE.
  • Score: Checks slope of the log-likelihood at equal rates.

If the drug improves survival, all three tests give low p-values. For borderline effects, results may differ slightly. Practitioners often rely on the LRT in multi-parameter settings, while regression outputs frequently report Wald tests. All are part of the same likelihood-based inference family.

Likelihood theory provides not only estimates and intervals but also hypothesis tests. The LRT is a powerful and general method, usable for comparing nested models (e.g., with or without certain predictors). The Wald and score tests provide computational convenience and complementary insights. Understanding their similarities and differences helps in interpreting results in medical research with more clarity.

Related Articles