Epidemiology / HEOR Analytics / Observational Data Analytics

Likelihood Ratios and Confidence Intervals

A likelihood ratio (LR) in this context is a tool to compare how well two different values of a parameter explain the observed data. Specifically, we often compare any given value to the best-fitting value (the MLE). The likelihood ratio for a particular value of the parameter is defined as:

LR = \frac{\text{Likelihood at a given parameter value}}{\text{Likelihood at the MLE}}

Because the likelihood at the MLE is the highest possible likelihood, any other value will have a likelihood ratio less than or equal to 1. An LR of 1 means the parameter value is just as likely as the MLE given the data (which only happens when the value is the MLE). An LR of 0.5, for example, would mean the data are half as likely under that parameter value compared to the MLE. The lower the likelihood ratio, the less the data support that parameter value.

It might help to think of the likelihood ratio as a relative measure of support: it tells you how many times less likely the data would be if the parameter had some other value instead of the MLE. Researchers often work with the logarithm of the likelihood (the log-likelihood) because it simplifies calculations, but the concept remains one of comparing heights of the likelihood function at different points.

Supported vs. Unsupported Values

Using likelihood ratios, we can define a range of “supported” values for our parameter – values for which the data are reasonably compatible. If the likelihood ratio is high (close to 1), the value is nearly as supported as the MLE by the data. If it’s very low, the data do not support that value much at all. We usually decide on a threshold ratio to determine what “supported” means.

For example, consider again the household TB transmission scenario from the previous article. The MLE for the risk p was 0.25 (25%). Let’s evaluate how the likelihood of the observed data (3 positives, 9 negatives out of 12) compares for some different values of p:

  • At the MLE, 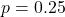p = 0.25: The likelihood ratio LR = 1 by definition. This is the top of the mountain – the best supported value.
  • At 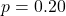p = 0.20 (20% risk): Plugging into 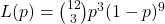L(p) = \binom{12}{3} p^3 (1-p)^9, we find L(0.20)/L(0.25) \approx 0.92. The data support 20% fairly well.
  • At p = 0.30 (30% risk): The ratio is around 0.93, so 30% is also almost as supported as 25%.
  • At 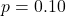p = 0.10 (10% risk): The ratio is about 0.33, meaning the observed result is only one-third as likely if the true risk were 10% compared to 25%.
  • At 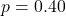p = 0.40 (40% risk): The likelihood ratio is around 0.55, showing less support but not impossible.
  • At p = 0.60 (60% risk): The LR is very low (around 0.05). Such a high transmission risk is strongly rejected by the data.

From these, we see that values of p roughly between 0.20 and 0.30 produce high likelihood ratios (close to 1), meaning the data support them nearly as well as they support the MLE of 0.25. Values far from that (like 0.10 or 0.60) produce low likelihood ratios, meaning those values are not supported by the data.

We can visualize this by imagining a curve of the likelihood ratio across all possible p. It starts at 0 when p=0, rises to 1 at p=0.25, and then goes back down towards 0 as p approaches 1. All values above a certain ratio threshold can be considered the “supported range” of p.

Likelihood Ratios and Confidence Intervals

The concept of a supported range of parameter values based on a likelihood ratio cutoff turns out to be closely related to a confidence interval. A confidence interval (CI) provides a range of values within which the true parameter likely falls, given a certain confidence level (like 95%). Usually we compute confidence intervals using statistical formulas, but you can also derive them using likelihoods.

For large samples, if the model assumptions are reasonable, choosing a particular likelihood ratio cutoff corresponds to a particular confidence level:

  • 95% CI: take all values with 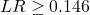LR \geq 0.146 (≈14.6%).
  • 90% CI: use a cutoff 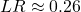LR \approx 0.26 (≈26%).
  • 99% CI: use a cutoff LR \approx 0.036 (≈3.6%).

In our TB example, the maximum likelihood was around 0.258 (in terms of raw likelihood value). The likelihood ratio of 0.146 corresponds to the cutoff for 95% support. So we’d find where L(p) = 0.146 \times L_{\max}. Those p values would mark the 95% confidence limits.

If we carry out the calculation (or use standard formulas for a binomial proportion CI), we might find roughly that the 95% CI for the true household transmission risk p goes from about 0.05 (5%) to 0.54 (54%). This is just an illustration – the exact numbers would come from solving L(p) = 0.146 \times L_{\max}.

Why Use Likelihood Ratios?

Likelihood ratios provide a consistent way to interpret data evidence across many types of problems: proportions, means, odds ratios, etc. They do not depend on the scale of the parameter – whether we describe an effect as a probability, an odds, a log-odds, or a risk ratio, the comparison is always based on relative likelihood.

By using the LR approach, researchers can derive confidence intervals without relying on traditional approximations that might fail if sample sizes are small or assumptions are shaky. Instead, one finds the supported range directly from the data’s likelihood function. This approach is fundamental in modern epidemiological analysis, especially with complex models where analytic formulas for CIs are not straightforward.

In summary, the likelihood ratio helps us move from a single best estimate (MLE) to an understanding of what other values are plausible. If an estimated risk or rate is 2.0 (for instance, a risk ratio), the likelihood ratio approach might show that values from 1.5 to 2.7 are well supported (forming a confidence interval), whereas values like 1.0 or 4.0 are not. This gives a more complete picture for clinicians and epidemiologists making decisions based on the data.

Related Articles