Predictive Analytics • Updated On July 29, 2025

Understanding Cross-Validation and Model Assumptions in Predictive Analytics

When you build a predictive model, success is not just about finding the right algorithm. It begins with understanding your data and validating the assumptions that shape your model. If these assumptions are ignored, the predictions may look accurate on paper but fail when exposed to new data. This guide will walk you through the essential steps of data preparation, cross-validation, and model performance evaluation in simple and practical terms.

Checking Model Assumptions Through Data Exploration

The first step for any analyst is to explore the data thoroughly. This involves looking for patterns, clusters, or anomalies that might influence your model. For example, a dataset of patient records might have groups of patients with similar symptoms, or it might include outliers such as extreme lab results. Identifying these patterns early prevents misleading conclusions.

Key tasks include:

Checking for skewness in distributions.
Detecting outliers that can distort averages.
Looking for nonlinear relationships that might require alternative models or transformations.

If the assumptions underlying a chosen model are violated, you may need to transform variables (e.g., taking logarithms for highly skewed data) or switch to a more robust modeling approach.

Dimension Reduction and Why It Matters

In high-dimensional datasets, not all variables carry equal weight. Too many variables can create noise and lead to overfitting. Techniques like Principal Component Analysis (PCA) or factor analysis simplify data by reducing variables to smaller sets of uncorrelated components, while preserving most of the original information.

For instance, if you have ten overlapping health metrics like blood sugar levels, body weight, and cholesterol, PCA can combine these into fewer representative factors. This approach improves both interpretability and computational efficiency.

Cross-Validation: The Backbone of Model Evaluation

Cross-validation (CV) is one of the most widely used methods to measure how well a model will generalize to new data. The goal is to estimate the Mean Squared Error (MSE) or other performance metrics by simulating how the model behaves on unseen data.

k-Fold Cross-Validation

In k-fold cross-validation (CV), the dataset is split into $k$ equal parts or folds. The model is trained on $k - 1$ folds and tested on the remaining fold. This process is repeated $k$ times, with each fold serving as the test set once.

A typical choice for $k$ is 5 or 10, though leave-one-out CV (LOOCV) is also common when $k = n$ , where $n$ is the total number of data points.

The CV Mean Squared Residual

The cross-validated mean square residual (CVMSR) is computed to evaluate prediction error. It is a better estimate of the true MSE than simply relying on training residuals.

The formula for MSE is:
$\text{MSE} = \frac{1}{n} \sum_{i=1}^{n} (y_i - \hat{y}_i)^2$

Where $y_i$ is the observed value and $\hat{y}_i$ is the predicted value.

In cross-validation (CV), each $\hat{y}_i$ is obtained from a model that does not include the $i$ -th data point in training. This prevents overfitting and gives a more realistic picture of performance.

Why Cross-Validation Works

Cross-validation ensures that every observation is used for both training and validation. This reduces the risk of overfitting, where the model performs well on training data but fails to generalize.

When selecting models, you can compare different algorithms or sets of predictors by minimizing CVMSR. For example, in all-subsets regression, the model with the lowest CVMSR is chosen as the best fit. This approach often outperforms traditional selection criteria like Mallows’ $C_p$ .

Training-Test Split vs. Cross-Validation

Another popular approach is splitting data into training and test sets. The training set is used to build the model, while the test set serves as a hold-out set to assess performance.

Training set: Used for model fitting and parameter estimation.
Test set: Represents unseen data and is only used for final evaluation.

Bishop (1995) suggested this as a practical approach to model validation. To ensure reliability, it is common to repeat the random split multiple times and average the test results.

Bias, Variance, and the MSE Decomposition

Understanding the components of error helps you design better models. The MSE can be decomposed as:

$\text{MSE} = \underbrace{\text{Variance}}<em data-start="4681" data-end="4726">{\text{noise}} + \underbrace{\text{Bias}^2}</em>{\text{model error}} + \underbrace{\text{Estimation Variance}}_{\text{parameter uncertainty}}$

This is summarized in Equation 4.1 (adapted from Hastie et al., 2009):
$\mathbb{E}[(Y - \hat{f}(x))^2] = \sigma^2 + \big( \mathbb{E}[\hat{f}(x)] - f(x) \big)^2 + \mathbb{E}\big[ (\hat{f}(x) - \mathbb{E}[\hat{f}(x)])^2 \big]$
where:

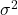$\sigma^2$ is the irreducible variance of the response $Y$ .
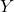The second term is the squared bias due to model assumptions,
The third term is the variance of the estimator.

Reducing bias often increases variance, and vice versa. The trick is to find the sweet spot where MSE is minimized.

Overfitting and Variability

A complex model might fit the training data perfectly but fail on new data. For example, if you build a highly flexible machine learning model to predict hospital readmissions, it might capture random noise in historical data instead of true patterns. This is why both CV and test sets are vital.

Repeating the CV or train-test split with multiple random partitions (e.g., 5–20 iterations) helps reduce the variability of the performance estimate.

The Role of Noisy Data

When the outcome $Y$ has high variance due to noise, even advanced nonlinear models like neural networks may not outperform simpler models. In such cases, the irreducible error $\sigma^2$ dominates the MSE, making further model complexity ineffective.

Imagine building a model to predict blood pressure from factors like age, weight, and diet. If you skip checking for outliers (e.g., patients with rare genetic conditions), your model might mislead you. Cross-validation can help you understand whether your model’s predictions hold up across different patient groups. By minimizing CVMSR across multiple folds, you ensure that the model is not simply memorizing patterns from the training data.