Biostatistics / Public Health • Updated On August 17, 2025

Confidence Intervals for Risk Ratios

When you work with medical or public health data, you often need to compare risks between two groups. A simple way to do this is through the risk ratio, sometimes called relative risk. But the risk ratio is only an estimate from your sample. To understand how reliable that estimate is, you need a confidence interval. This interval gives you a range of values that are consistent with the data and helps you judge whether the association is likely to be real or just due to chance. Previously we saw basics of risk ratios. In this article you will learn how confidence intervals for risk ratios are built, why logarithms are used, and how to interpret the results in practice.

Why Ratio Measures Need Special Handling

For most statistics, the procedure is straightforward. You calculate the standard error of the estimate, multiply it by the appropriate critical value, and add or subtract this product from the point estimate. For a 95 percent confidence interval, the critical value from the normal distribution is 1.96. In formula form, the confidence interval is

$CI = q \pm 1.96 \times SE(q)$

where $q$ is your estimate and $SE(q)$ is its standard error. This works well when the estimate can take both positive and negative values, such as a difference in risks. But the risk ratio can never be negative. When the sample is small or the estimate is close to zero, the normal approximation can produce lower limits that are negative, which makes no sense. To avoid this, researchers work with the logarithm of the risk ratio. The log of any positive number can be negative, zero, or positive, and the distribution of log ratios tends to be closer to normal. Once the interval for the log ratio is calculated, you simply transform it back to the original scale with the exponential function.

Step by Step Procedure

To calculate a confidence interval for the risk ratio you follow these steps:

First compute the risk ratio 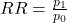$RR = \frac{p_1}{p_0}$ from your two groups.
Take the natural logarithm of the risk ratio. This is written as $\log(RR)$ .
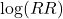Calculate the standard error of the log risk ratio. The formula is:

$SE(\log RR) = \sqrt{\frac{1}{d_1} - \frac{1}{n_1} + \frac{1}{d_0} - \frac{1}{n_0}}$

Here $d_1$ is the number of events in the exposed group, $n_1$ is the total size of the exposed group, $d_0$ is the number of events in the unexposed group, and $n_0$ is the total size of the unexposed group.

Build a confidence interval for the log risk ratio as $\log RR \pm 1.96 \times SE(\log RR)$ .
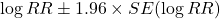Transform the limits back to the original scale by taking the exponential. This produces the confidence interval for the risk ratio.

The result is always positive, which is consistent with the definition of a ratio.

Introducing the Error Factor

Instead of writing all steps every time, researchers use a shortcut called the error factor. The error factor is defined as

$EF = \exp(1.96 \times SE(\log RR))$

The 95 percent confidence interval for the risk ratio can then be written in a compact form as

$CI(RR) = \left(\frac{RR}{EF}, RR \times EF\right)$

The error factor is always greater than one, because the exponential of a positive number is greater than one. This makes the confidence interval symmetrical on the log scale but asymmetrical on the ratio scale, which matches the way ratios behave in reality.

A Worked Example with Exercise and Diabetes

Let us consider a study of physical activity and risk of diabetes. Imagine two groups of adults are followed for five years. One group of fifteen thousand people engages in at least 150 minutes of exercise per week. Another group of fifteen thousand people reports minimal exercise. During follow up, 120 cases of diabetes occur in the active group, while 240 cases occur in the inactive group. The data are shown in Table 1.

Table 1. Hypothetical data on exercise and diabetes
Group	Diabetes	No diabetes	Total	Risk
Active	120	14,880	15,000	$p_1 = 120/15000 = 0.008$
Inactive	240	14,760	15,000	$p_0 = 240/15000 = 0.016$
Total	360	29,640	30,000	–

The risk ratio is $RR = 0.008 / 0.016 = 0.5$ . People who exercised regularly had half the risk of developing diabetes compared to those who did not.

Step 1. Calculate the log risk ratio

$\log RR = \log(0.5) = -0.693$

Step 2. Standard error of the log risk ratio

$SE(\log RR) = \sqrt{\frac{1}{120} - \frac{1}{15000} + \frac{1}{240} - \frac{1}{15000}}$

This simplifies to about 0.115.

Step 3. Calculate the error factor

$EF = \exp(1.96 \times 0.115) = \exp(0.225) = 1.252$

Step 4. Build the confidence interval

The 95 percent confidence interval is

$CI(RR) = (0.5 / 1.252, 0.5 \times 1.252)$

This equals (0.40, 0.63). You can interpret this as follows: the true protective effect of exercise lies somewhere between a 37 percent reduction and a 60 percent reduction in diabetes risk. Because the entire interval is below one, you have strong evidence that regular exercise is protective.

Testing the Null Hypothesis

To formally test whether the risk ratio differs from one, you use the log risk ratio and its standard error. The test statistic is

$z = \frac{\log RR}{SE(\log RR)}$

For the example, $z = -0.693 / 0.115 = -6.02$ . The corresponding p value is less than 0.0001, which is very strong evidence against the null hypothesis that exercise has no effect on diabetes risk.

Why Logs and Antilogs Matter

You may wonder why we go through the trouble of using logarithms. The reason is that ratios are skewed on their natural scale. A ratio of 0.5 and a ratio of 2 are not equally far from 1, but on the log scale they are mirror images, -0.693 and 0.693. This symmetry makes the normal approximation work much better. Once you transform back, you obtain a confidence interval that never goes below zero and respects the logic of ratios. The rules of logarithms and exponentials make the process smooth. For example, $\exp(\log a) = a$ , and $\exp(a + b) = \exp(a)\exp(b)$ . These shortcuts help in simplifying the algebra.

Interpreting the Results in Context

A confidence interval for a risk ratio is not just a statistical number, it tells a story. In the exercise study, the point estimate was 0.5. But the confidence interval, ranging from 0.40 to 0.63, gives you the range of plausible values. It rules out the possibility of no effect or an increased risk. In real practice, this interval would give researchers confidence to say that exercise is likely protective against diabetes, and policy makers might use such evidence to design preventive programs. The interpretation is straightforward: values below one suggest protection, values above one suggest increased risk, and if the interval crosses one the evidence is inconclusive.

Practical Considerations

When sample sizes are large, the confidence interval tends to be narrow, giving precise estimates. When events are rare or groups are small, the interval can be wide, showing great uncertainty. In those cases, researchers sometimes use exact methods or Bayesian approaches. But the log transformation method described here is the standard in most applied studies, because it is simple, interpretable, and robust for a wide range of situations.

Comparisons with Other Measures

It is important to see how confidence intervals for risk ratios differ from those for risk differences. For differences, you can directly apply the normal formula without worrying about negative limits, because the difference can be negative. For ratios, however, ignoring the log transformation can give misleading or impossible results. The method described here ensures the interval is mathematically sound and clinically meaningful.

Broader Use of Ratio Measures

Risk ratios are only one type of ratio measure. Similar methods apply to rate ratios and prevalence ratios. The same idea holds: take the logarithm, calculate the standard error, build the interval, and transform back. This is why you often see relative measures reported with asymmetric intervals in research papers. Once you know the logic, the approach becomes routine across many applications.

Key Points to Remember

Always use the log transformation when building confidence intervals for risk ratios.
The error factor provides a simple shortcut to calculate the limits.
Interpret intervals relative to the value one, which represents no association.
A narrow interval means precise evidence, while a wide interval suggests uncertainty.
The method generalizes to other ratio measures beyond risk ratios.

With practice, you will find this process intuitive. It allows you to move beyond a single number and see the full range of possible effects, which is the real value of confidence intervals in medical research.